مقدمة
هل صحيح أن الماء يُشعل الشموع؟ نعم، هذا صحيح!
هل صحيح أن الثعابين تخاف من الزرنيخ الأحمر؟ هذا غير صحيح!
ما سنناقشه اليوم هو:
هل يمكن أن يؤدي التداخل إلى تحسين دقة القياس؟
في الظروف العادية، يُعدّ التداخل عدوًا طبيعيًا للقياس، إذ يُقلّل من دقته. وفي الحالات الشديدة، قد يتعذّر إجراء القياس بشكل طبيعي. من هذا المنظور، يُفترض أن التداخل يُحسّن دقة القياس، وهذا غير صحيح!
لكن، هل هذا هو الحال دائماً؟ هل هناك حالة لا يؤدي فيها التداخل إلى تقليل دقة القياس، بل إلى تحسينها؟
الجواب هو نعم!
2. اتفاقية التداخل
وبالنظر إلى الوضع الراهن، نتوصل إلى الاتفاق التالي بشأن التدخل:
- لا يحتوي التداخل على مكونات تيار مستمر. في القياس الفعلي، يكون التداخل في الغالب تداخل تيار متردد، وهذا الافتراض معقول.
- بالمقارنة مع جهد التيار المستمر المقاس، فإن سعة التداخل صغيرة نسبياً. وهذا يتوافق مع الوضع الفعلي.
- التداخل إشارة دورية، أو أن متوسط قيمتها يساوي صفرًا خلال فترة زمنية محددة. هذه النقطة ليست بالضرورة صحيحة في القياسات الفعلية. مع ذلك، ولأن التداخل عادةً ما يكون إشارة تيار متردد عالية التردد، فإن افتراض متوسط صفري يُعدّ منطقيًا لفترة زمنية أطول في معظم حالات التداخل.
3. دقة القياس في ظل التداخل
تستخدم معظم أجهزة القياس الكهربائية والعدادات حاليًا محولات تناظرية رقمية، وترتبط دقة قياسها ارتباطًا وثيقًا بدقة المحول التناظري الرقمي. وبشكل عام، تتميز المحولات التناظرية الرقمية ذات الدقة الأعلى بدقة قياس أعلى.
مع ذلك، فإن دقة التحويل التناظري الرقمي محدودة دائمًا. بافتراض أن دقة التحويل التناظري الرقمي هي 3 بتات وأن أعلى جهد قياس هو 8 فولت، فإن هذا التحويل يُعادل مقياسًا مُقسّمًا إلى 8 أقسام، كل قسم منها يُمثل 1 فولت. نتيجة قياس هذا التحويل التناظري الرقمي هي دائمًا عدد صحيح، ويتم دائمًا الاحتفاظ بالجزء العشري أو تجاهله، وهو ما يُفترض الاحتفاظ به في هذه الورقة. سيؤدي الاحتفاظ بالجزء العشري أو تجاهله إلى أخطاء في القياس. على سبيل المثال، 6.3 فولت أكبر من 6 فولت وأصغر من 7 فولت. نتيجة قياس التحويل التناظري الرقمي هي 7 فولت، وهناك خطأ مقداره 0.7 فولت. نُطلق على هذا الخطأ اسم خطأ تكميم التحويل التناظري الرقمي.
ولتسهيل التحليل، نفترض أن المقياس (محول AD) ليس لديه أخطاء قياس أخرى باستثناء خطأ التكميم AD.
الآن، نستخدم مقياسين متطابقين لقياس جهدي التيار المستمر الموضحين في الشكل 1 بدون تداخل (الحالة المثالية) ومع التداخل.
كما هو موضح في الشكل 1، يبلغ جهد التيار المستمر المقاس فعليًا 6.3 فولت، وهو ثابت في الشكل الأيسر دون أي تداخل. أما الشكل الأيمن فيُظهر التيار المستمر متأثرًا بالتيار المتردد، مع وجود تذبذب طفيف في قيمته. ويتساوى جهد التيار المستمر في الشكل الأيمن مع نظيره في الشكل الأيسر بعد إزالة إشارة التداخل. ويمثل المربع الأحمر في الشكل نتيجة تحويل محول الإشارة التناظرية إلى الرقمية.

جهد تيار مستمر مثالي بدون تداخل
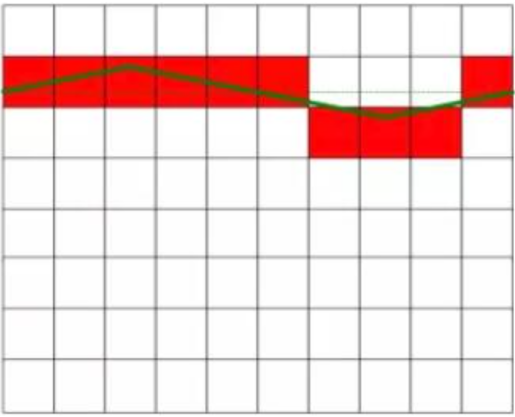
قم بتطبيق جهد تيار مستمر متداخل بقيمة متوسطة تساوي صفرًا
قم بإجراء 10 قياسات للتيار المستمر في الحالتين الموضحتين في الشكل أعلاه، ثم قم بحساب متوسط القياسات العشرة.
تم قياس المقياس الأول على اليسار عشر مرات، وكانت القراءات متطابقة في كل مرة. وبسبب تأثير خطأ التكميم التناظري الرقمي، كانت كل قراءة 7 فولت. وبعد حساب متوسط القياسات العشر، بقيت النتيجة 7 فولت. إذن، خطأ التكميم التناظري الرقمي هو 0.7 فولت، وخطأ القياس هو 0.7 فولت.
لقد تغير المقياس الثاني على اليمين بشكل كبير:
بسبب اختلاف جهد التداخل وسعته (موجبًا وسالبًا)، يختلف خطأ التكميم التناظري الرقمي (AD) باختلاف نقاط القياس. ومع تغير هذا الخطأ، تتراوح قيمة القياس بين 6 و7 فولت. كانت سبع من القياسات 7 فولت، وثلاث منها 6 فولت، بينما كان متوسط القياسات العشرة 6.3 فولت! وبالتالي، فإن الخطأ يساوي صفر فولت!
في الواقع، لا يوجد خطأ مستحيل، لأنه في العالم الموضوعي، لا يوجد جهد 6.3 فولت دقيق! ومع ذلك، توجد بالفعل:
في حالة عدم وجود تداخل، وبما أن كل نتيجة قياس هي نفسها، فبعد حساب متوسط 10 قياسات، يظل الخطأ دون تغيير!
عند وجود قدر مناسب من التداخل، وبعد حساب متوسط 10 قياسات، ينخفض خطأ التكميم التناظري الرقمي بمقدار عشرة أضعاف! وتتحسن الدقة بمقدار عشرة أضعاف! كما تتحسن دقة القياس بمقدار عشرة أضعاف!
الأسئلة الرئيسية هي:
هل يكون الأمر نفسه عندما تكون قيمة الجهد المقاسة مختلفة؟
قد يرغب القراء في اتباع الاتفاقية المتعلقة بالتداخل في القسم الثاني، والتعبير عن التداخل بسلسلة من القيم العددية، وتركيب التداخل على الجهد المقاس، ثم حساب نتائج القياس لكل نقطة وفقًا لمبدأ الحمل لمحول AD، ثم حساب القيمة المتوسطة للتحقق، طالما أن سعة التداخل يمكن أن تتسبب في تغيير القراءة بعد تكميم AD، وأن تردد أخذ العينات مرتفع بما فيه الكفاية (تغيرات سعة التداخل لها عملية انتقال، بدلاً من قيمتين موجبة وسالبة)، ويجب تحسين الدقة!
يمكن إثبات أنه طالما أن الجهد المقاس ليس عددًا صحيحًا تمامًا (أي أنه غير موجود في الواقع)، فسيكون هناك خطأ في تكميم المحول التناظري الرقمي، بغض النظر عن حجم هذا الخطأ. طالما أن سعة التداخل أكبر من خطأ التكميم أو أكبر من الحد الأدنى لدقة المحول، فسيؤدي ذلك إلى تغير نتيجة القياس بين قيمتين متجاورتين. ولأن التداخل متناظر موجَّهًا وسالبًا، فإن مقدار واحتمالية الانخفاض والزيادة متساويان. لذلك، عندما تكون القيمة الفعلية أقرب إلى قيمة معينة، فإن احتمالية ظهور تلك القيمة تكون أكبر، وستكون قريبة من تلك القيمة بعد حساب المتوسط.
أي أن: القيمة المتوسطة لعدة قياسات (القيمة المتوسطة للتداخل تساوي صفرًا) يجب أن تكون أقرب إلى نتيجة القياس بدون تداخل، أي أن استخدام إشارة تداخل التيار المتردد ذات القيمة المتوسطة تساوي صفرًا وحساب متوسط عدة قياسات يمكن أن يقلل من أخطاء التكميم التناظري الرقمي المكافئ، ويحسن دقة قياس التناظري الرقمي، ويحسن دقة القياس!
تاريخ النشر: 13 يوليو 2023




